Григорий Яковлевич Перельман родился 13 июня 1966 года в Ленинграде. Отец был
инженером-электриком, в 1993 году эмигрировал в Израиль. Мама преподавала математику в
училище.
С пятого класса Григорий Перельман посещал математический центр для одарённых детей при
Дворце пионеров под руководством Сергея Рукшина. В 1982 году в составе команды советских
школьников Перельман завоевал золотую медаль на Международной математической
олимпиаде в Будапеште.
Юный математик закончил 239-ю физико-математическую школу Ленинграда. Без вступительных экзаменов был принят в Ленинградский университет. За отличную учёбу получал Ленинскую стипендию. Поступил в аспирантуру при Ленинградском отделении Математического института им. В. А. Стеклова (ПОМИ). Защитив кандидатскую диссертацию, остался работать в институте старшим научным сотрудником.
В конце 1980-х стал работать научным сотрудником в США.
В 1996 году вернулся в Санкт-Петербург, продолжил работу в ПОМИ. Получил премию
Европейского математического общества для молодых математиков, но отказался её получать.
В 2002 году Перельман опубликовал работу, посвящённую решению одного из частных случаев
гипотезы геометризации Уильяма Тёрстона, из которой следует справедливость знаменитой
гипотезы Пуанкаре, сформулированной французским математиком, физиком и философом Анри Пуанкаре в 1904 году. Описанный учёным метод изучения потока Риччи получил название теории Гамильтона — Перельмана.
В декабре 2005 года ушёл с поста ведущего научного сотрудника лаборатории математической
физики, уволился из ПОМИ.
В 2006 году отказался от международной премии "Медаль Филдса" /названа в честь канадского
математика Джона Филдса/ за решение гипотезы Пуанкаре.
Журнал Science назвал доказательство теоремы Пуанкаре научным «прорывом года»
(«Breakthrough of the Year»).
Сильвия Назар написала статью «Manifold Destiny», которая рассказывает о Григории
Перельмане и математическом сообществе и содержит интервью с ним.
В 2007 году британская газета The Daily Telegraph опубликовала список 100 ныне живущих
гениев, в котором Григорий Перельман занимает 9-е место.
18 марта 2010 года Математический институт Клэя объявил о присуждении Григорию
Перельману премии в размере 1 миллион долларов США за доказательство гипотезы Пуанкаре.
8 июня 2010 года в Париже состоялась математическая конференция, на которой должна была
быть вручена «Премия тысячелетия». Перельман на вручение не приехал. Учредитель премии Джеймс Карлсон объявил, что он готов ждать решения Перельмана «столько, сколько
потребуется».
Книгу о Григории Перельмане написала Маша Гессен «Perfect Rigor: A Genius and the
Mathematical Breakthrough of the Century».
Гипотеза Пуанкаре
В исходной форме гипотеза Пуанкаре утверждает, что:
Обобщённая гипотеза Пуанкаре
Обобщённая гипотеза Пуанкаре утверждает, что:
Исходная гипотеза Пуанкаре является частным случаем обобщённой гипотезы при n = 3.
Доказательство гипотезы Пуанкаре
Поток Риччи — это определённое уравнение в частных производных, похожее на уравнение теплопроводности. Он позволяет деформировать риманову метрику на многообразии, но в процессе деформации возможно образование «сингулярностей» — точек, в которых кривизна стремится к бесконечности, и деформацию невозможно продолжить. Основной шаг в доказательстве состоит в классификации таких сингулярностей в трёхмерном ориентированном случае. При подходе к сингулярности поток останавливают и производят «хирургию» — выбрасывают малую связную компоненту или вырезают «шею» (то есть, вложенное  ), а полученные две дырки заклеивают двумя шарами так, что метрика полученного многообразия становится достаточно гладкой — после чего продолжают деформацию. Классификация сингулярностей позволяет заключить, что каждый «выброшенный кусок» диффеоморфен сферической пространственной форме. Процесс, описанный выше, называется «поток Риччи с хирургией».
), а полученные две дырки заклеивают двумя шарами так, что метрика полученного многообразия становится достаточно гладкой — после чего продолжают деформацию. Классификация сингулярностей позволяет заключить, что каждый «выброшенный кусок» диффеоморфен сферической пространственной форме. Процесс, описанный выше, называется «поток Риччи с хирургией».
При доказательстве гипотезы Пуанкаре начинают с произвольной римановой метрики на односвязном трёхмерном многообразии M и применяют к нему поток Риччи с хирургией. Важным шагом является доказательство того, что в результате такого процесса «выбрасывается» всё. Это означает, что исходное многообразие M можно представить как набор сферических пространственных форм S3 / Γi, соединённых друг с другом трубками ![[0,1] imes S^2](http://upload.wikimedia.org/math/5/f/a/5fa16609cb23083805b2834a727de096.png) . Подсчёт фундаментальной группы показывает, что Mдиффеоморфно связанной сумме набора пространственных форм S3 / Γi и более того все Γi тривиальны. Таким образом, M является связной суммой набора сфер, то есть, сферой.
. Подсчёт фундаментальной группы показывает, что Mдиффеоморфно связанной сумме набора пространственных форм S3 / Γi и более того все Γi тривиальны. Таким образом, M является связной суммой набора сфер, то есть, сферой.

Обложка журнала
Science№ 314(5807), 2006 год, провозглашающая доказательство гипотезы Пуанкаре «прорывом года».
Гипотеза сформулирована французским математиком Пуанкаре в 1904 году. Попытки доказать гипотезу Пуанкаре привели к многочисленным продвижениям в топологии многообразий.
Доказательства обобщённой гипотезы Пуанкаре для 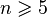 получены в начале 1960—1970-х почти одновременно Смейлом, независимо и другими методами Столлингсом (англ.) (для
получены в начале 1960—1970-х почти одновременно Смейлом, независимо и другими методами Столлингсом (англ.) (для  , его доказательство было распространено на случаи n = 5 и 6Зееманом (англ.)). Доказательство значительно более трудного случая n = 4 было получено только в 1982 году Фридманом (англ.). Из теоремы Новикова о топологической инвариантности характеристических классов Понтрягина следует, что существуют гомотопически эквивалентные, но не гомеоморфные многообразия в высоких размерностях.
, его доказательство было распространено на случаи n = 5 и 6Зееманом (англ.)). Доказательство значительно более трудного случая n = 4 было получено только в 1982 году Фридманом (англ.). Из теоремы Новикова о топологической инвариантности характеристических классов Понтрягина следует, что существуют гомотопически эквивалентные, но не гомеоморфные многообразия в высоких размерностях.
Википедия



